Particle Flow Map

Leapfrog Flow Maps for Real-Time Fluid Simulation

June 5, 2025 | Yuchen Sun

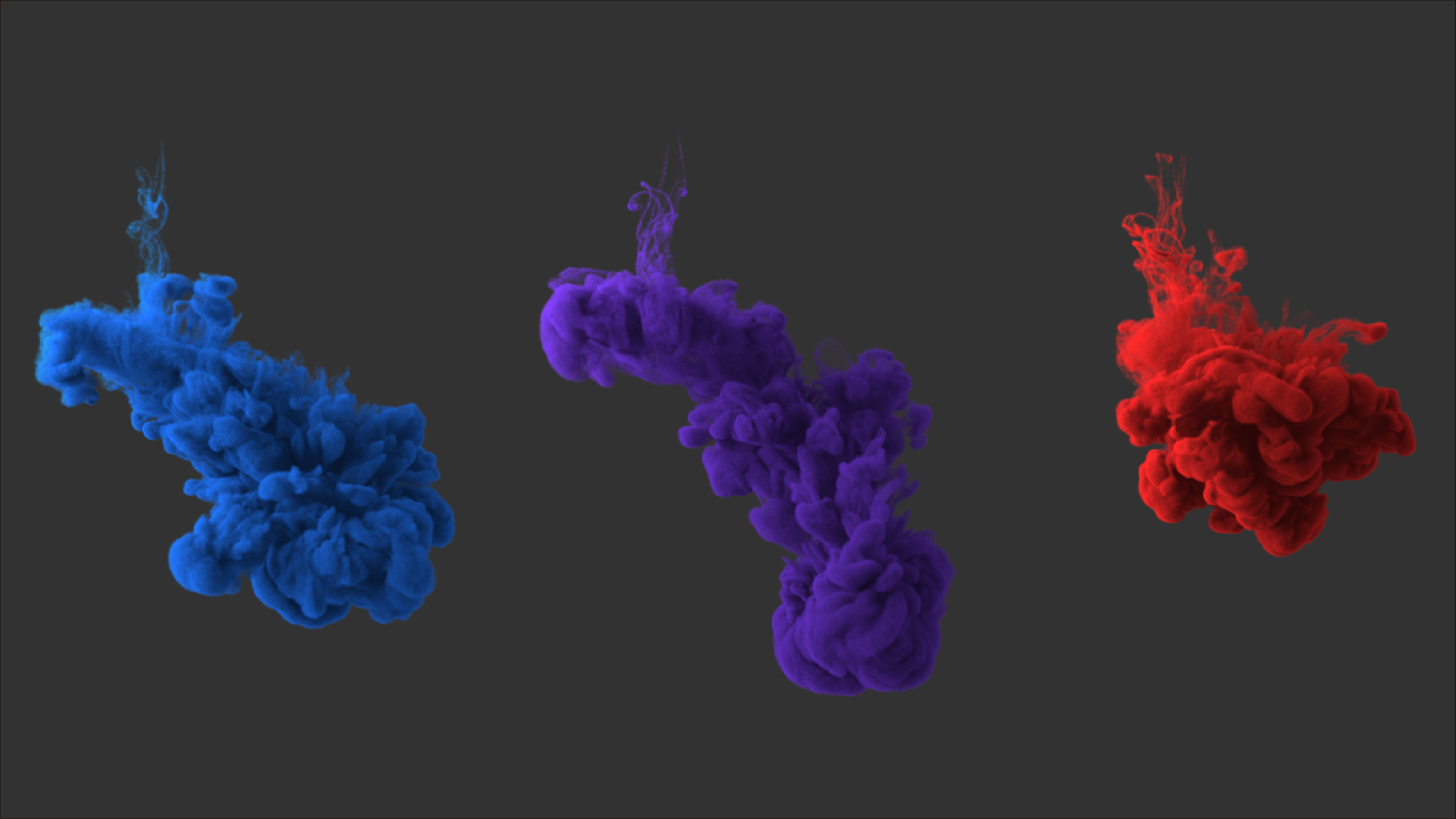
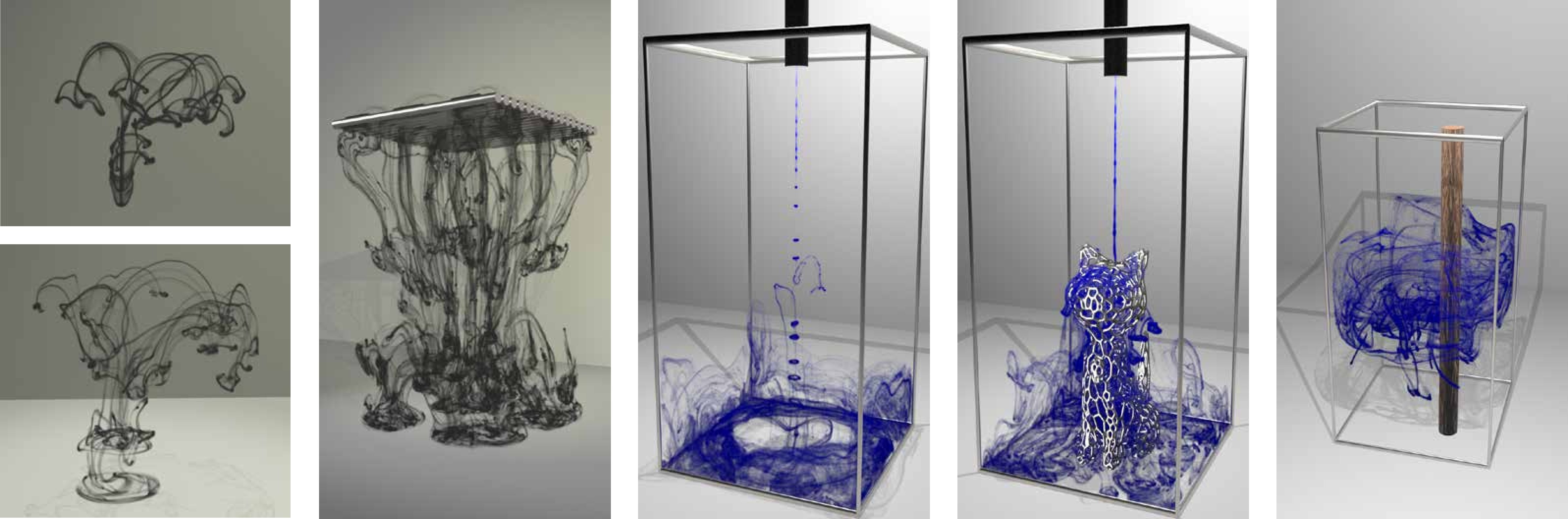
📢 We’re excited to share that our paper, “Leapfrog Flow Maps for Real-Time Fluid Simulation,” co-authored with Dr. van Bloemen Waanders from DOE Sandia National Laboratories, has just been accepted to SIGGRAPH 2025! Leapfrog Flow Maps (LFM) combine velocity and impulse updates via a leapfrog integrator, and all the heavy lifting is handled by a matrix-free AMGPCG solver tuned for GPUs. The result? Real-time delta-wingtip vortex simulations at 256 × 128 × 128 resolution on a single RTX 4090.
Key highlights from our paper:
📌 A hybrid velocity-impulse time integrator to reduce both the projection times and the flow-map marching steps
📌 A fast matrix-free Algebraic Multigrid Preconditioned Conjugate Gradient (AMGPCG) solver on GPU
📌 Large-scale fluid simulations in real time, such as fire balls and delta wingtip vortices
📌 Open-source code now available to the community
See our paper and code for more details!

📄 Paper Website & Preprint
🎞️ Simulation and validation videos
💻 Source Code

Full Abstract
We propose Leapfrog Flow Maps (LFMs) to simulate incompressible fluids with rich vortical flows in real-time. Our key idea is to utilize a hybrid velocity-impulse scheme, enhanced with the leapfrog method, to reduce the computational workload of impulse-based flow map methods while maintaining a strong ability to preserve vortical structures and fluid details. To accelerate the impulse-to-velocity projection, we develop a fast matrix-free Algebraic Multigrid Preconditioned Conjugate Gradient (AMGPCG) solver with customized GPU optimization, which makes the projection comparable to impulse evolution in terms of time cost. We demonstrate the performance of our method and its efficacy in a wide range of examples and experiments, including real-time simulated burning fireballs and delta wingtip vortices.

Next Steps
Following this work, we will continue our collaborative efforts by further exploring real-time CFD techniques, providing high-speed and high-fidelity simulation solutions to address various vorticity-dominant flow phenomena. Combustive dynamics on flow maps will be one of our particular focuses for the next steps.

Fluid Simulation on Compressible Flow Maps

June 5, 2025 | Duowen Chen

Exciting news—our paper “Fluid Simulation on Compressible Flow Maps”, in collaboration with Dr. van Bloemen Waanders from DOE Sandia National Laboratories, has been accepted to SIGGRAPH 2025! 🎉🎉🎉
In this work, we bring existing flow-map techniques under one roof, handling phenomena from tiny water-striders skimming pond surfaces to ships on vast oceans and even a Dragon capsule’s descent onto Mars. We’ve validated our solver against standard JCP benchmarks, demonstrating accuracy on par with high-order WENO methods for supersonic compressible flows, while simultaneously improving vorticity preservation in shallow-water and weakly compressible scenarios.
Key highlights from our paper:
✅Vortices perservation for Shallow Water Equation simulation.
✅Comparable accuracy with WENO schemes for high-Mach compressible flows under classical JCP benchmarks.
✅Simulation of different Mach numbers from 0.2 to 6 Mach within same framework
✅Weakly compressible simulation for typical incompressible cases (e.g., smoke, ink torus breakup).

Check out our full paper and simulation video for more details! Stay tuned to our code release!

📄 Paper Preprint
🎞️ Simulation and validation videos
💻 Source Code [Coming Soon]

Full Abstract
This paper presents a unified compressible flow map framework designed to accommodate diverse compressible flow systems, including high-Mach-number flows (e.g., shock waves and supersonic aircraft), weakly compressible systems (e.g., smoke plumes and ink diffusion), and incompressible systems evolving through compressible acoustic quantities (e.g., free-surface shallow water). At the core of our approach is a theoretical foundation for compressible flow maps based on Lagrangian path integrals, a novel advection scheme for the conservative transport of density and energy, and a unified numerical framework for solving compressible flows with varying pressure treatments. We validate our method across three representative compressible flow systems, characterized by varying fluid morphologies, governing equations, and compressibility levels, demonstrating its ability to preserve and evolve spatiotemporal features such as vortical structures and wave interactions governed by different flow physics. Our results highlight a wide range of novel phenomena, from ink torus breakup to delta wing tail vortices and vortex shedding on free surfaces, significantly expanding the range of fluid systems that flow-map methods can handle.

Next Steps
Following this preliminary study, we will continue our collaborative efforts to develop a high-fidelity combustion simulator by coupling incompressible and compressible flow map solvers, aiming to capture a wide range of vorticity-induced combustion dynamics and vortical structures. Particular emphasis will be placed on extending the current solver to large-scale domains for simulating real-world flow phenomena.

Clebsch Gauge Fluid on Particle Flow Maps

June 6, 2025 | Zhiqi Li

It's a pleasure to report that our work, “Clebsch Gauge Fluid on Particle Flow Maps”, has just been accepted to SIGGRAPH 2025 with Best Paper Award Honorable Mention! 🎉🎉🎉
Our Clebsch Gauge-based flow map solver uses 0-form wave functions as the mapping object of the flow map, addressing the long-standing challenges in advecting gradients in PFM. It successfully preserves strong vorticity even at low resolutions (32~64 grid size), without introducing significant time or memory overhead.
Here are the standout points from our work:
🌟 Clebsch-Based PFM Framework: By leveraging the point-based nature of Clebsch wave functions, we establish a new PFM framework that achieves state-of-the-art performance in vorticity-preserving simulations, and can reproduce classical vortex ring structures even at extremely low resolutions.
🌟 Gauge Transformation for Clebsch Wave Functions: We develop a novel gauge transformation that aligns the evolution of Clebsch wave functions with the particle flow map (PFM) framework, enabling accurate advection of scalar quantities and their gradients.
🌟 Velocity Reconstruction Scheme: We introduce a robust method for converting Clebsch wave functions into velocity fields, significantly improving simulation accuracy and fidelity in vorticity-dominated scenarios.

🎞️ Simulation and validation videos
💻 Source Code [Coming Soon]

Full Abstract
We propose a novel gauge fluid solver that evolves Clebsch wave functions on particle flow maps (PFMs). The key insight underlying our work is that particle flow maps exhibit superior performance in transporting point elements—such as Clebsch components—compared to line and surface elements, which were the focus of previous methods relying on impulse and vortex gauge variables for flow maps. Our Clebsch PFM method incorporates three main contributions: a novel gauge transformation enabling accurate transport of wave functions on particle flow maps, an enhanced velocity reconstruction method for coarse grids, and a PFM-based simulation framework designed to better preserve fine-scale flow structures. We validate the Clebsch PFM method through a wide range of benchmark tests and simulation examples, ranging from leapfrogging vortex rings and vortex reconnections to Kelvin–Helmholtz instabilities, demonstrating that our method outperforms its impulse- or vortex-based counterparts on particle flow maps, particularly in preserving and evolving small-scale features.

EDGE: Epsilon-Difference Gradient Evolution for Buffer-Free Flow Maps

June 6, 2025 | Zhiqi Li

It’s a pleasure to report that our work, “EDGE: Epsilon-Difference Gradient Evolution for Buffer-Free Flow Maps”, has just been accepted to SIGGRAPH 2025! 🎉🎉🎉
Our Epsilon Difference Gradient Evolution (EDGE) solver marries a Hermite-based flow-map approach with a tetrahedral epsilon-difference scheme to eliminate velocity buffers entirely. By combining first-order Gradient Evolution with this epsilon-difference trick, we collapse spatial complexity from O(n) to O(1), so you can trace flows over long paths without ever losing a hint of vorticity.
Here are the standout points from our work:
🌟 A buffer-free flow-map method with O(1) memory usage, independent of flow-map length, while preserving vorticity accuracy comparable to buffer-based approaches
🌟 A novel high-order advection scheme that evolves first-order derivatives and computes high-order mixed derivatives via the epsilon difference method, overcoming limitations of prior methods
🌟 A tetrahedron-based epsilon element scheme that further reduces computational cost, enabling efficient flow-map simulations

🎞️ Simulation and validation videos
💻 Source Code [Coming Soon]

Full Abstract
We propose the Epsilon Difference Gradient Evolution (EDGE) method for accurate flow-map calculation on grids via Hermite interpolation without using velocity buffers. Our key idea is to integrate Gradient Evolution for accurate first-order derivatives and a tetrahedron-based Epsilon Difference scheme to compute higher-order derivatives with reduced memory consumption. EDGE achieves O(1) memory usage, independent of flow map length, while maintaining vorticity preservation comparable to buffer-based methods. We validate our methods across diverse vortical flow scenarios, demonstrating up to 90% backward map memory reduction and significant computational efficiency, broadening the applicability of flow-map methods to large-scale and complex fluid simulations.

Cirrus: Adaptive Hybrid Particle-Grid Flow Maps on GPU

June 5, 2025 | Mengdi Wang

We are excited to announce that our paper "Cirrus: Adaptive Hybrid Particle-Grid Flow Maps on GPU" has been accepted to SIGGRAPH 2025! 🎉
Cirrus is a high-performance GPU fluid simulator that combines the best of both particle and grid-based methods. Our framework introduces a hybrid Eulerian-Lagrangian flow map representation, enabling adaptive simulation at resolutions up to 512×512×2048 on a single RTX 4090 GPU. It delivers high-quality vortex preservation with speedups up to 100× over uniform-grid baselines.
Key highlights from our paper:
✅ Fully adaptive flow map representation with particle-grid hybridization
✅ GPU-accelerated octree grid structure using 8×8×8 tiles
✅ Simulation of large-scale, high-vorticity scenarios such as vehicle wake flows and propeller-driven aircraft
✅ Open-source code now available to the community
Try it out and see the details below!

📄 Paper Website & Preprint
🎞️ Simulation and validation videos
💻 Source Code

Full Abstract
We propose the adaptive hybrid particle-grid flow map method, a novel flow-map approach that leverages Lagrangian particles to simultaneously transport impulse and guide grid adaptation, introducing a fully adaptive flow map-based fluid simulation framework. The core idea of our method is to maintain flow-map trajectories separately on grid nodes and particles: the grid-based representation tracks long-range flow maps at a coarse spatial resolution, while the particle-based representation tracks both long and short-range flow maps, enhanced by their gradients, at a fine resolution. This hybrid Eulerian-Lagrangian flow-map representation naturally enables adaptivity for both advection and projection steps. We implement this method in Cirrus, a GPU-based fluid simulation framework designed for octree-like adaptive grids enhanced with particle trackers. The efficacy of our system is demonstrated through numerical tests and various simulation examples, achieving up to 512×512×2048 effective resolution on an RTX 4090 GPU. We achieve a 1.5 to 2× speedup with our GPU optimization over the Particle Flow Map method on the same hardware, while the adaptive grid implementation offers efficiency gains of one to two orders of magnitude by reducing computational resource requirements.

Fluid Simulation on Vortex Particle Flow Maps

June 5, 2025 | Sinan Wang

We are thrilled to announce that our paper "Fluid Simulation on Vortex Particle Flow Maps" has been accepted to SIGGRAPH 2025! 🎉🎉🎉
Our work revisits the classical Vortex-In-Cell (VIC) method through a modern flow map perspective, extending traditional vortex particles into vortex particle flow maps that support long-term, stable, and accurate vortex evolution. By integrating higher-order information like vorticity gradients and flow map Hessians, we enable vortex-preserving simulations beyond the reach of existing methods. This approach successfully achieves stable flow maps 3–12× longer in various benchmarks, effectively re-establishing VIC as a competitive tool in graphics.
Key highlights:
✅ A vorticity-based particle flow map framework (VPFM) for fluid simulation.
✅ Introduction of flow map Hessians and higher-order vortex quantities for stable long-range flow maps (3–12× longer).
✅ Compatible boundary treatment in VPFM that supports no-through and approximated no-slip conditions.
✅ Revives the VIC method as a viable alternative to traditional velocity-based solvers in graphics.
Check out our full paper and simulation video for more details!

📄 Paper Preprint
🎞️ Simulation and validation videos
💻 Source Code [Coming Soon]

Full Abstract
We propose the Vortex Particle Flow Map (VPFM) method to simulate incompressible flow with complex vortical evolution in the presence of dynamic solid boundaries. The core insight of our approach is that vorticity is an ideal quantity for evolution on particle flow maps, enabling significantly longer flow map distances compared to other fluid quantities like velocity or impulse. To achieve this goal, we developed a hybrid Eulerian-Lagrangian representation that evolves vorticity and flow map quantities on vortex particles, while reconstructing velocity on a background grid. The method integrates three key components: (1) a vorticity-based particle flow map framework, (2) an accurate Hessian evolution scheme on particles, and (3) a solid boundary treatment for no-through and no-slip conditions in VPFM. These components collectively allow a substantially longer flow map length (3-12 times longer) than the state-of-the-art, enhancing vorticity preservation over extended spatiotemporal domains. We validated the performance of VPFM through diverse simulations, demonstrating its effectiveness in capturing complex vortex dynamics and turbulence phenomena.

Next Steps
After this preliminary investigation on applying the flow map scheme to vortex particles, we will continue to explore the efficacy of the VPFM method in simulating multi-scale and multi-physics problems. On the one hand, we will explore the potential of the significantly extended flow map lengths of vortex particles compared to other flow map techniques to facilitate multi-scale vortex structure evolution. On the other hand, we will focus on developing multi-physics coupling frameworks and investigating a variety of vortex–solid interaction phenomena. One of the primary objectives of our ongoing research is to extend the VPFM method from the computer graphics community to the broader computational physics community.

Six SIGGRAPH 2025 Papers on PFM!

June 1, 2025 | Bo Zhu

🚀 We are excited to share that our group has six journal papers accepted by SIGGRAPH 2025! These papers span a broad spectrum of topics centered around PFM, including incompressible and compressible flow simulations, hybrid particle-grid schemes, vortex particle methods, Clebsch flow maps, GPU multigrid and octrees, and buffer-free gradient techniques. In particular, we would like to highlight the two collaborative projects with the DOE's Sandia National Laboratory on building real-time and compressible flow-map solvers for high-fidelity and high-performance fluid simulators. These milestones reflect our group's ongoing efforts to advance PFM as a unifying simulation framework across computer graphics and scientific computing. Stay tuned for more results and open-source releases in the coming months!

📌 The accepted papers include:

• Leapfrog — A real-time incompressible flow-map solver with GPU-accelerated AMGPCG.
• Compressible — A unified flow-map framework for compressible, weakly compressible, and shallow water simulations.
• EDGE — A buffer-free gradient evolution method using epsilon-difference schemes.
• Cirrus — An adaptive hybrid particle-grid flow map simulator with octree acceleration on GPU.
• VPFM — A vorticity-based particle method for long-range vorticity structure tracking.
• Clebsch PFM — A Clebsch gauge representation for PFM.

An Impulse Ghost Fluid Method for Simulating Two-Phase Flows

June 5, 2025 | Yuchen Sun

🎉 We’re proud to share our latest work accepted at SIGGRAPH ASIA 2024! 🎉
In this paper, we present a two-phase fluid model driven by impulse dynamics that reproduces intricate flow behaviors with unmatched fidelity. By combining bidirectional flow maps with a cutting-edge ghost fluid method, we seamlessly integrate vorticity transport and interface motion within a single Eulerian framework. From swirling whirlpools to bubble-ring leapfrogging, our simulations bring these phenomena vividly to life.
Key highlights from our paper:
✅ A novel Impulse Ghost Fluid Method (IGFM) for simulating two-phase fluid
✅ A novel Path-Integral-Projection scheme to tackle the history-dependent jump of gauge variable on an Eulerian grid
✅ A novel Bidirectional-Marched-Flow-Map Level Set (BMFMLS) method to enhance volume preservation
✅ A two-phase flow solver to capture complex cross-interface vortex flow phenomena
Check out our paper for more details!

📄 Paper Website & Preprint
🎞️ Simulation and validation videos

Full Abstract
This paper introduces a two-phase interfacial fluid model based on the impulse variable to capture complex vorticity-interface interactions. Our key idea is to leverage bidirectional flow map theory to enhance the transport accuracy of both vorticity and interfaces simultaneously and address their coupling within a unified Eulerian framework. At the heart of our framework is an impulse ghost fluid method to solve the two-phase incompressible fluid characterized by its interfacial dynamics. To deal with the history-dependent jump of gauge variables across a dynamic interface, we develop a novel path integral formula empowered by spatiotemporal buffers to convert the history-dependent jump condition into a geometry-dependent jump condition when projecting impulse to velocity. We demonstrate the efficacy of our approach in simulating and visualizing several interface-vorticity interaction problems with cross-phase vortical evolution, including interfacial whirlpool, vortex ring reflection, and leapfrogging bubble rings.

Particle-Laden Fluid on Flow Maps

June 6, 2025 | Zhiqi Li

It's a pleasure to share that our work, "Particle-Laden Fluid on Flow Maps", has just been accepted to SIGGRAPH Aisa 2024 as Best Paper Award! 🎉
Our method introduces a novel framework for simulating ink as a particle-laden viscous flow, bridging the gap between classical flow maps and fully viscous Navier–Stokes simulations with drag and sediment coupling. It is capable of capturing intricate vorticity–viscosity interactions and reproducing a wide range of complex ink behaviors, including the bulging and breakup of viscous tails, the formation and disintegration of toroidal structures, and the coalescence and fractal-like branching of sedimenting drops. Here are the standout points from our work:
🌟 Our system faithfully reproduces ink tail breakup, torus formation and collapse, as well as fractal-like branching, capturing complex behaviors like vortex bulbs and hierarchical viscous structures.
🌟 We propose a novel path integral formulation for the Navier–Stokes equations that accurately incorporates viscosity and drag forces, enabling the simulation of dissipative particle-laden flows.
🌟 We introduce a new coupling mechanism that integrates long-range flow maps, short-range inter-particle forces, and a local projection step by solving variable-coefficient Poisson equations, achieving physically consistent interactions across scales.
🌟 We develop a unified Eulerian–Lagrangian solver for particle-laden flows, capable of delivering state-of-the-art ink diffusion simulations that capture intricate vorticity–viscosity interactions such as vortex bulbs, viscous tails, and hierarchical structures.

🎞️ Simulation and validation videos
💻 Source Code [Coming Soon]

Full Abstract
We propose a novel framework for simulating ink as a particle-laden flow using particle flow maps. Our method addresses the limitations of existing flow-map techniques, which struggle with dissipative forces like viscosity and drag, thereby extending the application scope from solving the Euler equations to solving the Navier-Stokes equations with accurate viscosity and laden-particle treatment. Our key contribution lies in a coupling mechanism for two particle systems, coupling physical sediment particles and virtual flow-map particles on a background grid by solving a Poisson system. We implemented a novel path integral formula to incorporate viscosity and drag forces into the particle flow map process. Our approach enables state-of-the-art simulation of various particle-laden flow phenomena, exemplified by the bulging and breakup of suspension drop tails, torus formation, torus disintegration, and the coalescence of sedimenting drops. In particular, our method delivered high-fidelity ink diffusion simulations by accurately capturing vortex bulbs, viscous tails, fractal branching, and hierarchical structures.

An Eulerian Vortex Method on Flow Maps

Dec 1, 2024 | Sinan Wang

Great news—our paper “An Eulerian Vortex Method on Flow Maps” has just been accepted to SIGGRAPH Asia 2024! 🎉🎉🎉
In this study, we unveil a grid-based vortex simulation built on flow maps—stepping away from classic Lagrangian or velocity-centric approaches. By marching vorticity back and forth across the mesh, we deliver both rock-solid stability and striking detail in swirling flows. At the heart of the technique lies a novel vorticity-to-velocity solver that imposes solid boundaries without ever touching a streamfunction, making it possible to capture rich behaviors like vortex leapfrogging, shedding, and tight solid–fluid dance—all within a pure Eulerian framework.
Key highlights:
🌟 An Eulerian vortex method that evolves vorticity directly on flow maps.
🌟 Bi-directional marching scheme for accurate flow map and Jacobian computation.
🌟 Matrix-free, GPU-friendly Poisson solver for velocity-vorticity reconstruction with boundary conditions.
🌟 Robust simulation results including vortex collisions, leapfrogging, and moving-solid vortex shedding.
Checkout our full paper and simulation video for more details!

📄 Paper
🎞️ Simulation and validation videos
💻 Source Code

Full Abstract
We present an Eulerian vortex method based on the theory of flow maps to simulate the complex vortical motions of incompressible fluids. Central to our method is the novel incorporation of the flow-map transport equations for line elements, which, in combination with a bi-directional marching scheme for flow maps, enables the high-fidelity Eulerian advection of vorticity variables. The fundamental motivation is that, compared to impulse 𝒎, which has been recently bridged with flow maps to encouraging results, vorticity 𝝎 promises to be preferable for its numerically stability and physical interpretability. To realize the full potential of this novel formulation, we develop a new Poisson solving scheme for vorticity-to-velocity reconstruction that is both efficient and able to accurately handle the coupling near solid boundaries. We demonstrate the efficacy of our approach with a range of vortex simulation examples, including leapfrog vortices, vortex collisions, cavity flow, and the formation of complex vortical structures due to solid-fluid interactions.

Solid-Fluid Interaction on Particle Flow Maps

Dec 1, 2024 | Duowen Chen

🔥🔥Checkout our recent published paper on SIGGRAPH ASIA 2024!🔥🔥
We introduce a path integral technique that solves the problem of perform two-way coupling between fluid and solid under flow map methods. At its heart are two clever tricks: an impulse-to-velocity transfer step that makes exchanging forces seamless, and a path-integral accumulation that carries coupling forces along each particle's trajectory. By converting impulse variable mapped through flow map to a divergent velocity field, we can easily couple with existing solid-fluid interaction methods such as MPM and IBM with only trivial modifications. We showcase the ability of our method with various test cases ranging from decending parachute to dropping leaf to swimming fish
Our key highlights:
📌 Provide a unified view that treats fluids and solids alike as particle flow maps.
📌 Reformulated impulse gauge fluid model and flow map techniques to snable solid fluid coupling.
📌 An easy approach that can be adopted to many coupling methods like IBM and MPM.
Checkout our full paper and simulation video for more details!

📄 Paper
🎞️ Simulation and validation videos
💻 Source Code

Full Abstract
We propose a novel solid-fluid interaction method for coupling elastic solids with impulse flow maps. Our key idea is to unify the representation of fluid and solid components as particle flow maps with different lengths and dynamics. The solid-fluid coupling is enabled by implementing two novel mechanisms: first, we developed an impulse-to-velocity transfer mechanism to unify the exchanged physical quantities; second, we devised a particle path integral mechanism to accumulate coupling forces along each flow-map trajectory. Our framework integrates these two mechanisms into an Eulerian-Lagrangian impulse fluid simulator to accommodate traditional coupling models, exemplified by the Material Point Method (MPM) and Immersed Boundary Method (IBM), within a particle flow map framework. We demonstrate our method's efficacy by simulating solid-fluid interactions exhibiting strong vortical dynamics, including various vortex shedding and interaction examples across swimming, falling, breezing, and combustion.

Eulerian-Lagrangian Fluid Simulation on Particle Flow Maps

July 19, 2024 | Junwei Zhou

🎉 We’re excited to announce that our latest work has been accepted to SIGGRAPH 2024! 🎉
In this paper, we introduce a novel Particle Flow Map (PFM) method that enables accurate long-range advection for incompressible fluid simulation. Built upon the insight that a forward-simulated particle trajectory naturally embodies a perfect flow map, we construct a hybrid Eulerian-Lagrangian solver that achieves state-of-the-art vorticity preservation while maintaining low memory cost and high computational efficiency.
Key highlights from our paper:
✅ A particle representation for long-range, bi-directional flow maps.
✅ A two-scale flow-map scheme, defined on a single particle trajectory, for mapping flow quantities with different reinitialization requirements.
✅ A particle-to-grid interpolation scheme to transfer flow maps from particles to grid nodes.
✅ A comprehensive Eulerian-Lagrangian solver based on the impulse fluid model, achieving state-of-the-art vorticity preservation capabilities while maintaining both low memory cost and high computational speed.

Feel free to try out our code and check out our simulation video below!

📄 Paper Website & Preprint
🎞️ Simulation and validation videos
💻 Soruce Code

Full Abstract
We propose a novel Particle Flow Map (PFM) method to enable accurate long-range advection for incompressible fluid simulation. The foundation of our method is the observation that a particle trajectory generated in a forward simulation naturally embodies a perfect flow map. Centered on this concept, we have developed an Eulerian-Lagrangian framework comprising four essential components: Lagrangian particles for a natural and precise representation of bidirectional flow maps; a dual-scale map representation to accommodate the mapping of various flow quantities; a particle-to-grid interpolation scheme for accurate quantity transfer from particles to grid nodes; and a hybrid impulse-based solver to enforce incompressibility on the grid. The efficacy of PFM has been demonstrated through various simulation scenarios, highlighting the evolution of complex vortical structures and the details of turbulent flows. Notably, compared to NFM, PFM reduces computing time by up to 49 times and memory consumption by up to 41%, while enhancing vorticity preservation as evidenced in various tests like leapfrog, vortex tube, and turbulent flow.